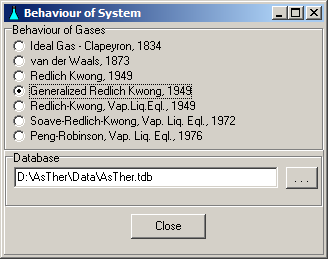
6. Algorithm of the Calculation in AsTher
6. 1. Behaviour of the System
When the critical constants Tc, Pc are known, the state functions can be calculated
using real gases rules.
The behaviour of the system can be selected separately in each AsTher application.
The Generalized Redlich-Kwong equation of state (1949) is set as default.
Menu System -> Behaviour shows a window, in which the equation of state
can be selected to calculation.

6.1.1. Ideal gas - Clapeyron, 1834
![]()
State Functions are calculated corresponding to the equations in Cap. 6.2.1
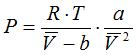
a = 27 . R2 .Tc2/( 64
. Pc )
b =R . Tc /( 8 . Pc )
State Functions are calculated corresponding to the equations in
Cap. 6.2.1
6.1.3. Redlich-Kwong, 1949
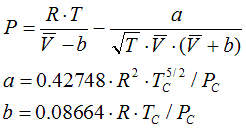
a = 0.42748 . R2 .Tc5/2 / Pc
b = 0.08664 .R .Tc / Pc
State Functions are calculated corresponding to the equations in Cap. 6.2.1
6.1.4. Generalized Redlich-Kwong, 1949
![]()
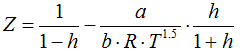
a = 0.42748 . R2 .Tc2 / Pc
b = 0.08664 .R .Tc / Pc
h = 0.08664 .R
.Tc /( Z . Pc )
State Functions are calculated corresponding to the equations in Cap. 6.2.1
6.1.5. Redlich-Kwong Vapour-Liquid-Equilibrium, 1949
State Functions, compressibility and liquid volume are calculated corresponding
to the equations in Cap. 6.2.2
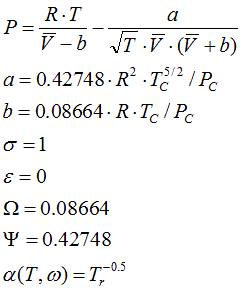
6.1.6. Soave Modification of Redlich-Kwong Vapour-Liquid-Equilibrium, 1972
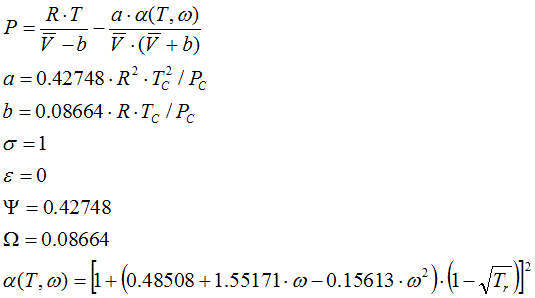
α(T,ω) equation is due to Graboski and Daubert.
State Functions, compressibility and liquid volume are calculated corresponding to the equations in Cap. 6.2.2
6.1.7. Peng Robinson Vapour-Liquid-Equilibrium, 1976
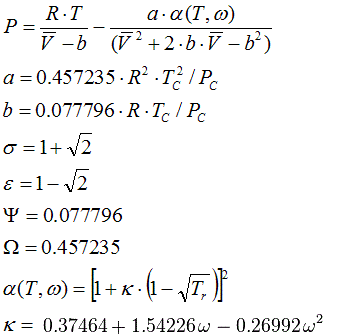
State Functions, compressibility and liquid volume are calculated corresponding to the equations in Cap. 6.2.2
Reference of the enthalpy values: enthalpy of elementar substances is zero at 25C and 1 bar in usual natural state.
The Cp –Function is calculated according to
Cp =
a + 10-3 .
b . T + 106 . c .
T -2 + 10-6 . d . T2
+ 109 . e . T -3 + 10-9
. f . T3
or
Cp =
a +
b . (T/1000) + c .
(T/1000) -2 + d . (T/1000)2
+ e . (T/1000) -3 + f .
(T/1000)3
a, b, c, d, e, f: empiric values in the AsTher Database from different sources, T [K]: Temperature.
If the constants are known according to the Shomate
Equation
Cp = A + B .(T/1000) + C .(T/1000)² + D
.(T/1000)³ + E .(T/1000)-²
then the constants can be replaced in AsTher database corresponding to the
following table
Important: Ref.-Field in the dataset must not contain "[<hgt>]",
when Shomate constants are
used in a dataset
| Constants in Shomate Equation |
equal to the constants in AsTher database |
| A | a |
| B | b |
| E | c |
| C | d |
| 0 (Zero) | e |
| D | f |
Important
The Constants for Shomate Equations from NIST can be
used directly in Asther-Database,
only when the reference Enthalpy and Entropy are in the range of the validity of
constants.
When the constants of the Cp function are valid at
temperature 298 [K],
then the constants can be directly used in the AsTher Database.
When the constants of the Cp function are valid
at the
temperature interval of 1000 -2000 [K],
then the constants can not be used in the AsTher Database
6.2.1. State functions in depend of specific heat capacity and compressibility
The molar enthalpy is calculated according to
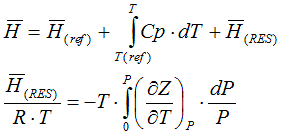
The molar entropy is calculated according to
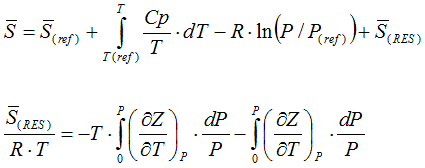
The molar free energy is calculated according to
![]()
6.2.2. Residual value of state function based on cubic equation of state
from Smith, Van Ness, and Abbott (Introduction to Chemical Engineering
Thermodynamics, 7th ed.)
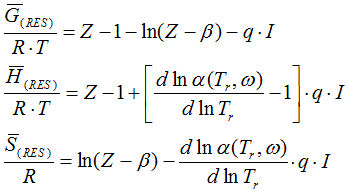
Z: compressibility for vapours:
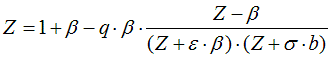
Z: compressibility for liquids:
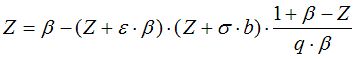
![]()
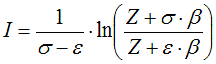
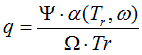
6.2.3. State functions based on correlation of measurements
In several datasets, the calculations of H(T) and G(T) base on the measured data
in small
temperature range in non-ideal equilibrium state, without the
Cp-correlation,
when reference is [<hgt>].
In such case.
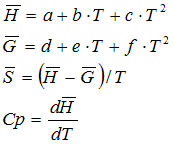
a, b, c, d, e, f: empiric values in the
AsTher Database according to different sources.
6.3. Extrapolation: when the extrapolation enabled,
the calculations are carried out outsides of the data range.
When the extrapolation is not enabled, the calculations will be not are carried
out and the reason is shown in the a messages window.
6.4.
Calculation of the Equilibrium in
the Application Equilibrium
The state of equilibrium is defined by following relations:
![]()
or
![]()
Free enthalpy of the pure substance at temperature and pressure of the thermodynamic system
ai: Activity of the compound in the thermodynamic system
fi :
Fugacity of the compound i in the thermodynamic system
R: Gas-constant T: Temperature
νe(i):
Number of atoms of the element e in the compound i in the thermodynamic system
λe: Lagrange-Coefficient of the element e in the thermodynamic system
For the mass balance, following relations is valid:
![]()
Ne: Mol number of the element e in the thermodynamic system
ni: Mol number of the compound i in the thermodynamic system
νe(i):
Number of atoms of the element e in the compound i
a A (s) + b B (g) = c C (l)
First calculate the equilibrium constant K using the calculated values of the partial pressures and/or activities:
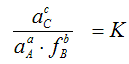
then calculate the equilibrium constant K via the Gibbs (free) energy:
![]()
Compare the K values from both equation
The Gibbs free energies can be calculated by the AsTher-Application Pure Substance at the given temperature of the system.
The change of the free energy can be calculated also by the AsTher-Application Reaction.
The results are allways within the selected accuracy.
Abs. 3.3. shows an example for the argumentation of consistency.